数据结构之线段树

发表于 | 更新于: | 分类于 ， | | 阅读数
字数统计: 2k | 阅读时长 ≈ 10

树状数组是一颗多叉树，而线段树是一颗平衡二叉树，两者多用于区间的操作

借用宫水三叶的总结：

数组不变，求区间和：「前缀和」、「树状数组」、「线段树」

多次修改某个数，求区间和：「树状数组」、「线段树」

多次整体修改某个区间，求区间和：「线段树」、「树状数组」（看修改区间的数据范围）

多次将某个区间变成同一个数，求区间和：「线段树」、「树状数组」（看修改区间的数据范围

这样看来，「线段树」能解决的问题是最多的，那我们是不是无论什么情况都写「线段树」呢？

答案并不是，而且恰好相反，只有在我们遇到第 4 类问题，不得不写「线段树」的时候，我们才考虑线段树。

因为「线段树」代码很长，而且常数很大，实际表现不算很好。我们只有在不得不用的时候才考虑「线段树」。

总结一下，我们应该按这样的优先级进行考虑：

简单求区间和，用「前缀和」
多次将某个区间变成同一个数，用「线段树」
其他情况，用「树状数组」

我来归纳一下：

数据结构\操作 区间求和 区间最大值 区间修改 单点修改
前缀和 √ × × ×
树状数组 √ √ × √
线段树 √ √ √ √
  • 只用到区间求和：前缀和
  • 区间求和+单点修改：树状数组
  • 区间修改：线段树

基本概念

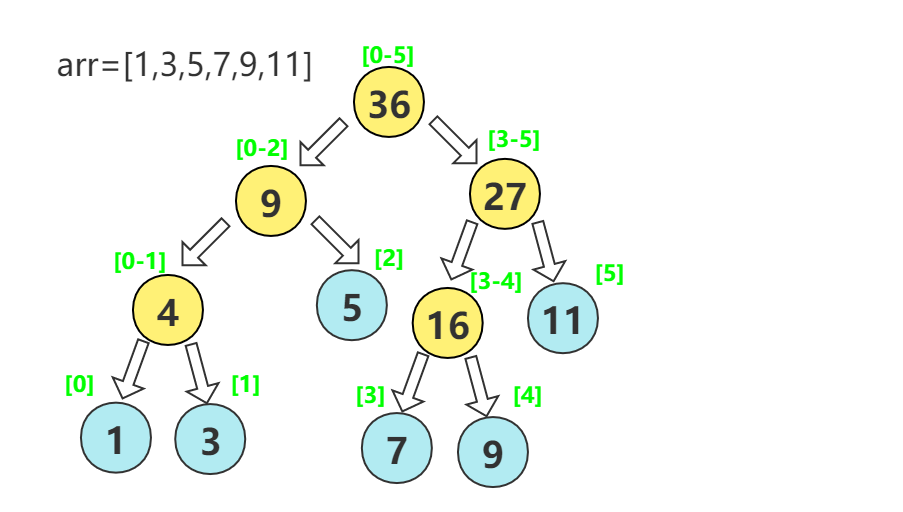
线段树是一棵平衡二叉树，母结点代表整个区间的和，越往下区间越小，叶节点长度为1，不可再分

线段树的每个节点都对应一条线段（区间），但并不保证所有的线段（区间）都是线段树的节点

节点 p的左右子节点的编号分别为2p和2p+1

假如节点p储存区间[a,b]的和，设$mid = \frac{l+r}{2}$那么两个子节点分别储存[l,mid]和[mid+1,r]的和

1002-1

懒标记

区间更新是线段树的灵魂之一（我是这么理解的😀），其中懒标记是关键

当我们对区间修改时，如果类似于单点修改那样一个个修改，那么复杂度太高(O(nlogn))，显然不合适

这时我们对每个区间加一个懒标记，标志着这个区间是否进行了修改，如果进行了，那么它的子区间也要进行修改，并且把懒标记转给子结点

关键之处在于，我们只传递了懒标记，但并不会真的去修改这些子节点（而是在用到这个子节点的时候再修改）

懒标记的实质：拖延修改，能懒则懒

代码模板

考虑到线段树的复杂性，因此给出了一个可以运行和调试的代码，并且每个变量都采用了易于理解的全称，每个区间均为闭区间

由于使用了数组模拟，并且考虑到虚点（也就是没有区间长度的点）的存在，因此需要开4倍的空间，如果被卡空间复杂度，可以考虑换成节点模拟+动态开点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
def main():
    nums=[1,3,5,7,9,11]	# examples
    n=len(nums)
    tree=[0]* 4*n   # TREE_SIZE
    
    def build(node,start,end):  # [start,end],后序创建二叉树
        if start==end:
            tree[node]=nums[start]
            return
        mid=start+end>>1
        lnode=2*node+1
        rnode=2*node+2
        build(lnode,start,mid)
        build(rnode,mid+1,end)
        tree[node]=tree[lnode]+tree[rnode]

    def update(node,start,end,idx,val):	# nums[idx]=>val
        if start==end:
            tree[node]=val
            return
        mid=start+end>>1
        lnode=2*node+1
        rnode=2*node+2
        if start<=idx<=mid:
            update(lnode,start,mid,idx,val)
        elif mid+1<=idx<=end:
            update(rnode,mid+1,end,idx,val)
        tree[node]=tree[lnode]+tree[rnode]	# 修改父节点

    def query(node,start,end,ql,qr): # sum [ql,qr]
        if ql>end or qr<start:
            return 0
        elif start>=ql and end<=qr:	# 剪枝
            return tree[node]
        elif start==end:
            return tree[node]

        mid=start+end>>1
        lnode=2*node+1
        rnode=2*node+2
        lsum=query(lnode,start,mid,ql,qr)
        rsum=query(rnode,mid+1,end,ql,qr)
        return lsum+rsum

    build(0,0,n-1)
    print(tree)
    update(0,0,n-1,4,6)	# nums[4]=>6
    print(tree)
    res=query(0,0,n-1,2,5)	# sum nums [2,5]
    print(res)	
    



if __name__ == '__main__':
    main()

区间更新：（这里放上了我自己总结的板子，每个人代码风格不一样，不用完全照搬）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
tree=[0]* 4*n
   lazy=[0]* 4*n
   def build(p,s,t):   # [s,t]
       if s==t:
           tree[p]=nums[s]
           return
       m=s+t>>1
       build(2*p+1,s,m)
       build(2*p+2,m+1,t)
       tree[p]=tree[2*p+1]+tree[2*p+2]

   def update(p,s,t,ul,ur,val): # [ul,ur]=val
       if ul<=s and t<=ur:
           tree[p]=(t-s+1)*val
           lazy[p]=val
           return
       m=s+t>>1
       if lazy[p] and s!=t:
           tree[2*p+1]=lazy[p]*(m-s+1)
           tree[2*p+2]=lazy[p]*(t-m)
           lazy[2*p+1]=lazy[p]
           lazy[2*p+2]=lazy[p]
           lazy[p]=0
       if ul<=m:
           update(p*2+1,s,m,ul,ur,val)
       if ur>m:
           update(p*2+2,m+1,t,ul,ur,val)
       tree[p]=tree[p*2+1]+tree[p*2+2]
       
   def query(p,s,t,ql,qr): # ask[ql,qr]
       if ql<=s and t<=qr:
           return tree[p]
       m=s+t>>1
       if lazy[p]:
           tree[p*2+1]=lazy[p]*(m-s+1)
           tree[p*2+2]=lazy[p]*(t-m)
           lazy[p*2+1]=lazy[p]
           lazy[p*2+2]=lazy[p]
           lazy[p]=0
       res=0
       if ql<=m:
           res+=query(2*p+1,s,m,ql,qr)
       if qr>m:
           res+=query(2*p+2,m+1,t,ql,qr)   
       return res
   
   
   def add(p,s,t,ul,ur,val): # [ul,ur]+=val
       if ul<=s and t<=ur:
           tree[p]+=(t-s+1)*val
           lazy[p]+=val
           return
       m=s+t>>1
       if lazy[p] and s!=t: # s==t为叶子节点
           tree[2*p+1]+=lazy[p]*(m-s+1)
           tree[2*p+2]+=lazy[p]*(t-m)
           lazy[2*p+1]+=lazy[p]
           lazy[2*p+2]+=lazy[p]
           lazy[p]=0
       if ul<=m:
           update(p*2+1,s,m,ul,ur,val)
       if ur>m:
           update(p*2+2,m+1,t,ul,ur,val)
       tree[p]=tree[p*2+1]+tree[p*2+2]

   def query2(p,s,t,ql,qr): # ask[ql,qr]
       if ql<=s and t<=qr:
           return tree[p]
       m=s+t>>1
       if lazy[p]:
           tree[p*2+1]+=lazy[p]*(m-s+1)
           tree[p*2+2]+=lazy[p]*(t-m)
           lazy[p*2+1]+=lazy[p]
           lazy[p*2+2]+=lazy[p]
           lazy[p]=0
       res=0
       if ql<=m:
           res+=query(2*p+1,s,m,ql,qr)
       if qr>m:
           res+=query(2*p+2,m+1,t,ql,qr)
       return res

无懒标记版本：

这个版本可以用来代替树状数组

tree=[0]*4*n
def build(p,s,t):
    if s==t:
        tree[p]=nums[s]
        return

    m=s+t>>1
    build(2*p+1,s,m)
    build(2*p+2,m+1,t)
    tree[p]=tree[2*p+1]+tree[2*p+2]

def update(p,s,t,idx,val):
    if s==t:
        tree[p]=val
        return
    m=s+t>>1
    if s<=idx<=m:
        update(2*p+1,s,m,idx,val)
    if m+1<=idx<=t:
        update(2*p+2,m+1,t,idx,val)
    tree[p]=tree[2*p+1]+tree[2*p+2]

def query(p,s,t,ql,qr):
    if ql<=s and t<=qr:
        return tree[p]
    m=s+t>>1
    res=0
    if ql<=m:
        res+=query(2*p+1,s,m,ql,qr)
    if qr>m:
        res+=query(2*p+2,m+1,t,ql,qr)
    return res

区域和检索 - 数组可修改

同样的题，昨天用树状数组写了一遍，今天可以用线段树来写了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class NumArray:

    def __init__(self, nums: List[int]):
        def build(node,start,end):
            if start==end:
                self.tree[node]=nums[start]
                return
            mid=start+end>>1
            lnode=2*node+1
            rnode=2*node+2
            build(lnode,start,mid)
            build(rnode,mid+1,end)
            self.tree[node]=self.tree[lnode]+self.tree[rnode]

        self.n=len(nums)
        self.tree=[0]*4*self.n
        build(0,0,self.n-1)

    def update(self, index: int, val: int) -> None:
        def _update(node,start,end,idx,val):
            if start==end:
                self.tree[node]=val
                return
            mid=start+end>>1
            lnode=2*node+1
            rnode=2*node+2
            if start<=idx<=mid:
                _update(lnode,start,mid,idx,val)
            else:
                _update(rnode,mid+1,end,idx,val)
            self.tree[node]=self.tree[lnode]+self.tree[rnode]
        
        _update(0,0,self.n-1,index,val)


    def sumRange(self, left: int, right: int) -> int:
        def query(node,start,end,ql,qr):
            if start>qr or end<ql:return 0
            elif start>=ql and end<=qr:return self.tree[node]
            elif start==end:return self.tree[node]
            
            mid=start+end>>1
            lnode=2*node+1
            rnode=2*node+2  
            lsum=query(lnode,start,mid,ql,qr)
            rsum=query(rnode,mid+1,end,ql,qr)     
            return lsum+rsum
        
        return query(0,0,self.n-1,left,right)




# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# obj.update(index,val)
# param_2 = obj.sumRange(left,right)
不要打赏，只求关注呀QAQ