数据结构之树状数组

发表于 | 更新于: | 分类于 ， | | 阅读数
字数统计: 2.1k | 阅读时长 ≈ 10

树状数组引入

一个数总可写成：$num=2^i + 2^j + 2^k,i<j<k$(参考二进制)

因此可以将[1,num]区间分成

$len=2^i:[1,2^i]$

$len=2^j:[2^i+1,2^j]$

$len=2^k:[2^j+1,2^k]$

树状数组（还有块状数组）就是这样将一个区间分成不同长度(一般长为2的幂次方)来进行维护的方法

  • 树状数组也叫 Binary Indexed Tree，二进制索引树，树状数组里某个元素管理了原始输入数组多少数据是由下标决定的
  • 树状数组通常用于动态的维护前缀数组
  • 树状数组的特点是区间查询和单点更新均为O(logn)

lowbit

先看一个例子：lowbit(44)=lowbit(101100B)=(100B)=4

可以发现

1
2
3
4
5
原码：101100
取反：010011
加一：010100

原码&取反+1：000100

所有，lowbit(i)=i&(~i+1)

考虑到计算机以补码的形式存储整数，所以lowbit(i)=i&(-i)

  • 当x为0时结果为0
  • x为奇数时，结果为1
  • x为偶数时，结果为x中2的最大次方的因子

树状数组和原数组

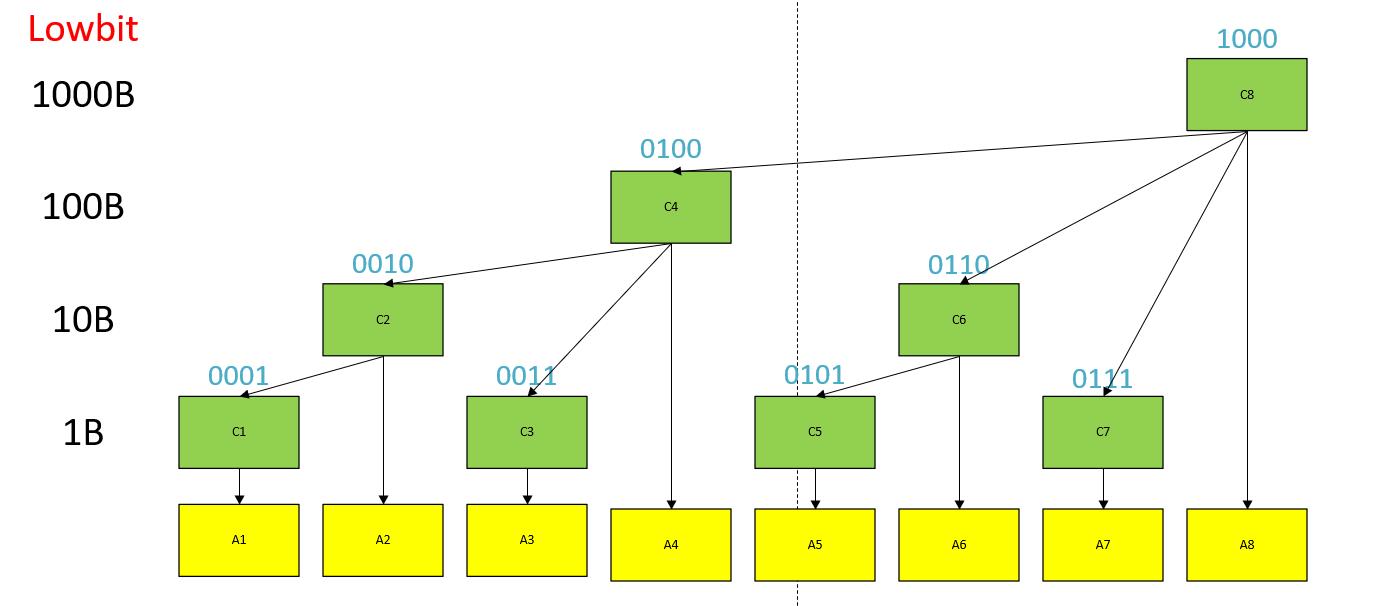
1001-1

数组数组与原数组关系：(注意数组数组下标从1开始)

1
2
3
4
5
6
7
8
C[1]=A[1]
C[2]=A[1]+A[2]
C[3]=A[3]
C[4]=A[1]+A[2]+A[3]+A[4]
C[5]=A[5]
C[6]=A[5]+A[6]
C[7]=A[7]
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]

总结规律，可以发现

C[i]=A[i-lowbit(i)+1] + …… + A[i]

单点更新，区间查询

更新时，需要同时更新A[i],A[i+lowbit(i)],A[i+2*lowbit(i)]……不超过最大值

求和时，则累加A[i]+A[i-lowbit(i)]+A[i-2*lowbit(i)]+……+A[1]

例如，add(3,5)，需要寻找父节点，同时对A[3],A[4],A[8]做+5，可以发现3+lowbit(3)=4,4+lowbit(4)=8

ask(7)时，需要寻找左上节点，同时对A[7],A[6],A[4]做累加，发现7-lowbit(7)=6,6-lowbit(6)=4

区间更新，单点查询

用树状数组维护一个差分数组b

【l,r】+d：add(l,d) and add(r+1,-d)

查询a[x]：ans=a[x]+ask[x]

ask[x]即为a[x]的增量

区间更新，区间查询

用2个数状数组维护

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class FenwickTree:
    def __init__(self,nums):
        self.nums=[0]+nums	# 为了下标从1开始
        n=len(nums)	# 注意是nums,原数组长度
        for i in range(1,n+1):	# O(n)时间的建立方法
            j=i+self.lowbit(i)
            if j<n+1:
                self.nums[j]+=self.nums[i]

    def lowbit(self,i):
        return i&(-i)

    def update(self,idx,val):
        prev=self.query(idx+1)-self.query(idx)	# 原数
        idx+=1	# 注意
        change=val-prev
        while idx<len(self.nums):
            self.nums[idx]+=change
            idx+=self.lowbit(idx)


    def query(self,idx):
        res=0
        while idx>0:
            res+=self.nums[idx]
            idx-=self.lowbit(idx)
        return res

或者这个由力扣官方题解给出的版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class BIT:
    def __init__(self, n):
        self.n = n
        self.a = [0] * (n + 1)

    def lowbit(x):
        return x & (-x)

    def query(self, idx):
        res = 0
        while idx > 0:
            res += self.a[idx]
            idx -= self.lowbit(idx)
        return res

    def add(self, idx, delta):
        while idx <= self.n:
            self.a[idx] += delta
            idx += self.lowbit(idx)

    def update(self,idx,val):
        prev=self.query(idx+1)-self.query(idx)
        change=prev-val
        self.add(idx,change)

以及我这个版本[🐕]

  1. 本体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def lowbit(i):
    return i&(-i)

def query(i):   # 找左上节点,sum(nums[:i])
    res=0
    while i>0:
        res+=base[i]
        i-=lowbit(i)
    return res

def add(i,val):  # 找父节点,nums[i-1]+val
    while i<=n:	 # 注意
        base[i]+=val
        i+=lowbit(i)


base=[0]*(n+1)
for i in range(n):  # 构造BIT,O(logn)构造时间
    add(i+1,nums[i])

"""
for i,v in enumerate(nums):
	add(i+1,v)
"""
  1. DLC
1
2
3
4
5
6
7
def update(self, index: int, val: int) -> None:	# set nums[i]=val
    prev=self.query(index+1)-self.query(index)
    change=val-prev
    self.add(index+1,change)    # 别忘了idx+1
    
def sumRange(self, left: int, right: int) -> int:
	return self.query(right+1)-self.query(left)

  1. 离散化

    考虑到「树状数组」的底层是数组（线性结构），为了避免开辟多余的「树状数组」空间，需要进行「离散化」；
    「离散化」的作用是：针对数值的大小做一个排名的「映射」，把原始数据映射到 [1, len] 这个区间，这样「树状数组」底层的数组空间会更紧凑，更易于维护

1
2
3
4
5
6
7
8
9
10
# 去重方便离散化
s = list(set(nums))

# 借助堆离散化
heapq.heapify(s)
rank_map=dict()
rank=1
while s:
    rank_map[heapq.pop(s)]=rank
    rank+=1
树状数组练习题库 力扣树状数组知识点题库

https://www.luogu.com.cn/problem/P3374

https://vjudge.net/problem/POJ-3468

参考文章

https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/solution/shu-zhuang-shu-zu-by-liweiwei1419/

https://www.cnblogs.com/xenny/p/9739600.html

区域和检索 - 数组不可变

这题可以直接用前缀和做

1
2
3
4
5
6
7
8
9
10
11
12
class NumArray:

    def __init__(self, nums: List[int]):
        self.pre=[0,*accumulate(nums)]

    def sumRange(self, left: int, right: int) -> int:
        return self.pre[right+1]-self.pre[left]


# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(left,right)

区域和检索 - 数组可修改

树状数组维护前缀和，直接用前缀和会超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class NumArray:

    def __init__(self, nums: List[int]):
        self.n=len(nums)
        self.base=[0]*(self.n+1)
        for i in range(self.n):
            self.add(i+1,nums[i])
        
    def update(self, index: int, val: int) -> None:
        prev=self.query(index+1)-self.query(index)
        change=val-prev
        self.add(index+1,change)    # 别忘了idx+1，考虑题目要求

    def sumRange(self, left: int, right: int) -> int:
        return self.query(right+1)-self.query(left)

    def query(self,i):
        res=0
        while i>0:
            res+=self.base[i]
            i-=(i&-i)
        return res
    
    def add(self,i,val):
        while i<=self.n:
            self.base[i]+=val
            i+=(i&-i)

# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# obj.update(index,val)
# param_2 = obj.sumRange(left,right)

面试题 10.10. 数字流的秩

朴素的想法就是用cnt[x]记录x的个数，x的秩就是sum(cnt[:x])

直接模拟会超时，所以用树状数组维护cnt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class StreamRank:

    def __init__(self):
        self.base=[0]*50010
    def track(self, x: int) -> None:
        def add(i,val):
            while i<=50010:
                self.base[i]+=val
                i+=(i&-i)

        add(x+1,1)

    def getRankOfNumber(self, x: int) -> int:
        def query(i):
            res=0
            while i>0:
                res+=self.base[i]
                i-=(i&-i)
            return res

        return query(x+1)

计算右侧小于当前元素的个数

上来就是一个单调栈，没有意外直接WA了

1
2
3
4
5
6
7
8
9
10
11
12
13
# 错误代码示范
class Solution:
    def countSmaller(self, nums: List[int]) -> List[int]:
        n=len(nums)
        res=[0]*n
        stack=[]
        for i in range(n-1,-1,-1):
            while stack and stack[-1]>=nums[i]:
                stack.pop()
            res[i]=len(stack)
            stack.append(nums[i])
        
        return res

因为单调栈的性质，只能用来求Next greater element，而非计数

这里应该用离散化+树状数组：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution:
    def countSmaller(self, nums: List[int]) -> List[int]:
        n=len(nums)
        # 特判
        if n== 0:
            return []
        if n == 1:
            return [0]

        base=[0]*(n+1)
        def lowbit(i):
            return i&(-i)
        
        def query(i):
            res=0
            while i>0:
                res+=base[i]
                i-=lowbit(i)
            return res
        
        def add(i,val):
            while i<=n:
                base[i]+=val
                i+=lowbit(i)
        
        # 离散化
        s=list(set(nums))
        heapq.heapify(s)
        rank_map=dict()
        rank=1
        while s:
            rank_map[heapq.heappop(s)]=rank
            rank+=1
        
        # 求解
        res=[0]*n
        for i in range(n-1,-1,-1):
            rank=rank_map[nums[i]]
            add(rank,1)
            res[i]=query(rank-1)
        return res

统计作战单位数

3元组问题，枚举中间点

直接枚举的时间复杂度为$O(n^2)$，显然不够好

用树状数组维护，可以达到O(nlogn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution:
    def numTeams(self, rating: List[int]) -> int:
        n = len(rating)
        def add(i, val):
            while i <= n:
                base[i] += val
                i += (i & -i)
        def query(i):
            res = 0
            while i > 0:
                res += base[i]
                i -= (i & -i)
            return res

        # 离散化
        s = list(set(rating))
        heapq.heapify(s)
        rank_map = dict()
        rank = 1
        while s:
            rank_map[heapq.heappop(s)] = rank
            rank += 1

		# 求解
        i_less,i_more = [0] * n,[0] * n
        base = [0] * (n + 1)
        for i, val in enumerate(rating):
            index = rank_map[val]
            i_less[i] = query(index)
            i_more[i] = i - i_less[i]
            add(index, 1)
            
        k_less,k_more = [0] * n,[0] * n
        base = [0] * (n + 1)
        for i in range(n - 1, -1, -1):
            index = rank_map[rating[i]]
            k_less[i] = query(index)
            k_more[i] = n - 1 - i - k_less[i]
            add(index, 1)
            
        ans = 0
        for i in range(n):
            ans += i_less[i] * k_more[i]
            ans += i_more[i] * k_less[i]
        return ans

总结

树状数组是维护区间的一个工具

你应该先想到一个结果数组，然后再设计树状数组去维护他

不要打赏，只求关注呀QAQ